RAI

RAI makes it possible to write VST/VSTi, Pd, and Jack Audio DSP code in Scheme.

The project is hosted on Github. To install, install Racket and run the following command.

See the Racket package manager documentation for more information.

1 Introduction

Racket Abstract Interpretation (RAI), is a code analysis and generation system built around a domain specific language (DSL).

The system allows for multiple abstract interpretations (AI) of programs expressed in the DSL. Some interpretations included are

• Scheme code for interactive exploration

• Dependency-free C code to run on small target systems

• linear(ized) transfer function for frequency analysis

• Automatic Differentiation

• Racklog program for logic analysis

• Symbolic mathematical expressions

DSL programs are represented as abstract syntax, parameterized by a structure describing the implementation of the language primitives. Writing a new interpretation involves the execution of a program parameterized by such a description, often in some form of context.

Program interpretations can be constructed to be composable, i.e. an iterpretation can transform a RAI program into another RAI program.

2 Time and Space

The language consists mostly of two parts, reflecting the qualitative difference of time and space dimensions.

• An arithmetic core that can be given both a scalar and a stream semantics, in that basic operators operate on scalar values or infinite stream values, possibly collected in finite, nested spatial arrays.

• A a collection of primitives that allows the creation of causal temporal relations, requiring a stream interpretation of the input/output data.

The design of the temporal primitives is motivated by applications from the domain of musical signal processing (music DSP). Such applications

• rely heavily on the composition of output feedback systems such as linear IIR filters and other state machines, and

• often use a parameter update scheme that executes at a lower sampling rate, i.e. the control rate.

The semantics of the full stream processing language is quite close to that of Faust.

3 Memory–less Operations

• Arithmetic operations: + - * / mod ^ floor sin cos exp log atan

• Bitwize logic operations and or xor not

• Predicates: <

• Finite array traversal with accumulator and array output: loop

• Scheme language forms: define lambda let let* let-values let*-values values

• Conditional: ?

• Standard Scheme forms for unrolled Metaprogramming

3.1 Composition

3.2 Iteration

The loop construct is a combination of map style list to list and fold style list to scalar operations. This primitive closely resembles the feedback mechanism for the time dimension.

As an illustration consider a program that takes an input array and computes the accumulated array.

#lang s-exp rai/stream

(define (sum xs)

(let-values*

(((accu-out array-out)  ;; accumulators and output arrays

(loop (i (n 3))       ;; loop index and array length

((accu 0))          ;; accumulators

((x xs))            ;; input element binding

(let* ((sum (+ acc x))

(out sum))

(values sum      ;; accumulator out

out))))) ;; array element out

array-out))

3.3 Conditional

Since the language is pure, the if operator is a function, and there is a lot of freedom on how to implement it.

In the low-level implementation used in C code generation, the computations in both branches are executed. Only the resulting value is selected based on the condition. This approach allows the language semantics to be mapped to data-parallel processing such as CPU SIMD instructions or GPU shaders.

Note that this choice prevents the use of direct recursion in the DSL. Recursion is currently not prevented, and will cause infinite loops. For the application domain, the need for recursion is mostly eliminated by the presence of the loop construct.

4 Causal Stream Operations

• Unit delay output-feedback form: feedback

• Support for variable length delay lines.

• Control-rate operators: hold setup

4.1 Unit Delay Feedback

Output feedback is specified using the feedback language primitive, or a small layer of syntactic sugar using the define form.

The feedback operator takes a pure operator (function) and transforms it into a causal stream operator. This abstraction corresponds to a canonical State space representation.

Here is how to express a discrete integrator using the special define form.

#lang s-exp rai/stream

(define (integrator (s) (x))

(let ((sum (+ s x)))

(values sum     ;; state update

sum)))  ;; system output

The state inputs are grouped separately from the ordinary inputs. The output of the function is the concatenation of state output and ordinary outputs.

It can be interpreted both on the stream level, where input and output streams correspond to shifted versions of each other, or at the scalar level where the next time step’s state vector and current output is computed based on the current state and input.

4.2 Delay Lines

In music DSP applications, a frequently used form of output feedback system is the delay line. An example of such a system would be

#lang s-exp rai/stream

(define (delay (s0 s1 s2 s3) (x))

(let* ((from-delay s3)

(to-delay (+ x (* 1/2 from-delay))))

(values to-delay s0 s1 s2  ;; state updates

to-delay)))        ;; output

This is a 4-tap delay line. Notice the pattern in the state output: all state variables are shifted by one, and the head of the line is updated with a new input, in this case a mix of input and delay output feedback.

In typical applications, the size of the delay state can grow very large. It makes sense to introduce an abstraction to make specification easier, and to also allow the extra annotation to guide a more efficient implementation. The approach taken in RAI is to abstract the delay line state as an indexable array, and to limit the construction of an updated delay state to the shift operation.

#lang s-exp rai/stream

(define (delay (s) (x))

(let* ((from-delay (dl-ref s 3))  ;; delay state vector indexed read

(to-delay (+ x (* 1/2 from-delay))))

(values (dl-shift s to-delay)  ;; delay state vector update

to-delay)))            ;; output

4.3 Control-rate operators

The hold and setup operators implement a limited form of subsampling, addressing very specific need in the target domain of audio DSP. In the future subsampling could be implemented in a more general way.

The subsampling factor is determined by the block rate of the system, meaning the number of audio samples processed in a single block for the VST, Pd and Jack interfaces.

The hold operator is a sample and hold operator. It will sample a value at the first time instance of a sample block and hold it for subsequent samples. The setup operator is similar, in that it will pass through its first argument at the first time instance, and its second argument at any other.

The combination of both allows the implementation of per-block computations, e.g. the computation of an expensive function evaluation running at control rate, driving a cheaper interpolation scheme running at audio rate. A good example of this is the computation of log scale control parameters in a sound synthesizer or effect, such as frequency or volume controls.

5 Unrolled Metaprogramming

In some cases it is desirable to specify an algorithm at a higher level using data structures and associated operations that are not supported on a target platform. E.g. in RAI the C target only supports operations on (nested) linear arrays, which is a straightforward translation of the loop construct.

In this case, ideally one would want to relate the higher level data structures and manipulations to some optimized combination of loops over arrays. A good example of this is the way in which loop fusion is performed in the Feldspar language. Such an approach requires a certain amount of trickery to be implemented. This is not yet possible in RAI.

Meanwhile, there is a simpler way to perform powerful code generation when one drops to manipulation of scalar values. This uses a correspondence between values at the meta level and individual (scalar) variable nodes at the target program level. This approach could be called the generation of flat or unrolled code.

The RAI language contains primitives for array construction and deconstruction that allows this form of flexible code generation to be combined with the C target’s array datastructures. The automatic array unpacking is performed in the map operator.

Keep in mind that while this can lead to efficient implementations if the unrolling exposes optimization opportunities, in general the unrolling can introduce a lot of code duplication if it is applied to large collections of compile-time data. When possible, it’s probably good to stick to consecutive applications of the loop construct to implement multi-pass array algorithms, as this translates to target-side loops over arrays.

6 Examples

6.1 Frequency analysis and C code generation

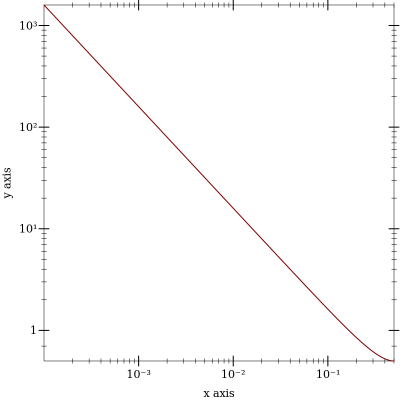
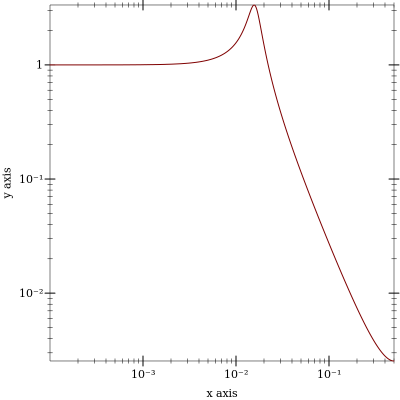
A typical use case is to define a filter, plot its transfer function, and when satisfied, generate some C code.

The filter can be defined in a separate module file or a submodule form exporting an identifier referring to the abstract program. This program can then be passed to an analysis or code generation function such as ai-spectrum or ai-array-c below. The former can be used in conjunction with Racket’s plot facility. The latter produces a C syntax file containing a C function, structure definitions for input, output and state, and preprocessor macros that abstract meta data to facilitate integration in a C host framework.

> (module test rai/stream     (provide svf integrator)     (define (integrator (s) (x))       (let ((s (+ s x)))         (values s s)))     (define (svf (s1 s2) (in))       (let* ((f 0.1)              (q 0.3)              (s2 (+ s2 (* f s1)))              (s1 (- s1 (* f (+ (* q s1) s2 in)))))         (values s1 s2                 s2))))

> (require 'test)

> (require rai/ai-freq)

> (require plot)

> (define (plot-filter f)     (parameterize       ((plot-x-transform log-transform)        (plot-y-transform log-transform)        (plot-x-ticks (log-ticks))        (plot-y-ticks (log-ticks)))     (plot (function             (compose magnitude                      (ai-spectrum f))             0.0001 0.5))))

> (plot-filter integrator)

> (plot-filter svf)

> (require rai/ai-array-c)

> (display (ai-array-c svf #:nsi 1))

struct proc_si {     int r5;     float r7;     float r8; }; #define proc_si_r5 0 #define proc_si_r7 0 #define proc_si_r8 0 #define proc_for_si(m) \     m(r5, 0, 1) \     m(r7, 0, 1) \     m(r8, 0, 1) \   struct proc_so {     int r6;     float r15;     float r10; }; #define proc_so_r6 0 #define proc_so_r15 0 #define proc_so_r10 0 #define proc_for_so(m) \     m(r6, 0, 1) \     m(r15, 0, 1) \     m(r10, 0, 1) \   struct proc_in {     float * restrict in; }; #define proc_in_in 0 #define proc_for_in(m) \     m(in, 0, 1) \   struct proc_param { }; #define proc_for_param(m) \   struct proc_out {     float * restrict r16; }; #define proc_out_r16 0 #define proc_for_out(m) \     m(r16, 0, 1) \   struct proc_store {     float r2[1]; }; #define proc_store_r2 1 #define proc_for_store(m) \     m(r2, 1, 1, 1) \   #define proc_for_control(m) \ void proc_loop (     struct proc_si * restrict state,     struct proc_in * restrict in,     struct proc_param * restrict param,     struct proc_out * restrict out,     struct proc_store * restrict store,     int t_endx) {     struct proc_si * restrict si = (struct proc_si *)(&state[(0)&1]);     struct proc_so * restrict so = (struct proc_so *)(&state[(1)&1]);     for (int t = 0; t < t_endx; t ++) {         struct proc_si * restrict si = (struct proc_si *)(&state[(t^0)&1]);         struct proc_so * restrict so = (struct proc_so *)(&state[(t^1)&1]);         /*?*/ float r0 = p_copy(t);         /*?*/ float r1 = p_copy(t_endx);         /*?*/ float r3 = p_copy(1.0);         /*?*/ float r4 = p_sub(r3, 1.0);         so->r6 = p_sub(si->r5, 1.0);         float r9 = p_mul(0.1, si->r7);         so->r10 = p_add(si->r8, r9);         float r11 = p_mul(0.3, si->r7);         float r12 = p_add(so->r10, in->in[t]);         float r13 = p_add(r11, r12);         float r14 = p_mul(0.1, r13);         so->r15 = p_sub(si->r7, r14);         out->r16[t] = p_copy(so->r10);     } }

7 Integrating C code

See the included "Makefile" and "rules.mk" files for an example of how to integrate generated C code in a host environment.

The following C/C++ files are combined with a generated header identfied by a ".g.h" extension to produce a binary output.

These files use the C preprocessor info and enumeration macros in the generated C file to construct data or code representations containing metadata for the target platform.

The SP module format is an ad-hoc run-time loadable binary format replacing the native dynamic library format. It is intended mainly for testing purposes.

8 TODO / Known Issues

• This project is in an experimental stage. There are many holes in the implementation. Also, the C code generator has gotten a bit quirky and needs a refactoring pass. That said, RAI is being used for real work.

• State threading for delay lines does not mix with the loop construct. Fixing this requires a better understanding of how to mix constants appearing on two levels: in type parameterizations and code.

• Subsampling and block processing in the time dimension needs to be cleaned up and generalized.